Many e-mail systems contain a spam detector that classifies mails in two categories: spam and not-spam (or ham). In this TD, you are going to implement your own spam detector, based on the \(k\)-NN algorithm. The algorithm relies on training data, that is, mails that are known for sure whether they are spam or ham. The SpamAssassin Public Corpus gives access to many labeled mails. We will use this corpus.
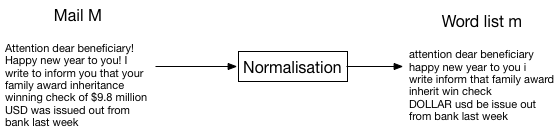
First, mails are pre-processed in order to obtain a normalized representation.
Pre-processing steps include:
removing the mail header;
putting all letters in lowercase;
replacing URLs, mail addresses, HTML tags, numbers, and dollars with explicit tags (URL, MAIL, HTML, NUM, DOLLAR);
reducing words to their root (sometimes called tokenization or lemmatization, e.g., birds becomes bird and called becomes call);
removing characters that are not words.

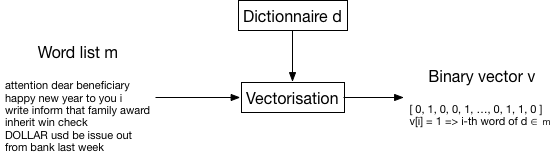
Once this pre-processing step has been completed, every mail is represented by a word list. These normalized mails can be used to create a dictionary containing all words that appear at least 100 times in the corpus. With the considered corpus, this creates a dictionary with 1899 items, i.e., there are 1899 words in the corpus that appear at least 100 times. We can arrange this dictionary so as to index it, e.g., alphabetically. Its first word has index 0, its last word has index 1898. Given the dictionary, a word is thus uniquely defined as its index in the dictionary.
Finally, every normalized mail \(m\) is transformed into a binary vector \(v\) of 1899 dimensions, as follows: \[\begin{equation} \forall i \in [\![0,1898]\!],~v[i] = 1 \iff \quad \text{the $i$-th word of the dictionary appears in the mail $m$} \end{equation}\]
You don’t need to perform the data pre-processing.
The data we provide you is in the form of labeled data, that is, the mails have already been pre-processed to the binary vector form. The data is separated in two files: mail_train.csv and mail_test.csv. The ham label is represented by integer 0, and the spam label is represented by integer 1. Note that labels (ham or spam, 0 or 1) are indicated in the first column of the row (the rest of columns indicates word features).
Remark: Since \(k\)-NN is a geometric method (i.e., it relies on distances between data points), you should have understood by now that the choice we made of representing e-mails as presence/absence of words of an ad hoc dictionary has a huge impact on how well we are able to classify them. In fact, most recent approaches to natural language processing (NLP), including spam-vs.-ham classification, focus on actually learning the best embedding (meaning, the best vector space to project e-mails to) of the text instead of choosing one a priori (which is what we did here: we chose to build a dictionary based on a threshold frequency of 100 appearances in a given corpus). For example, switching from the presence/absence of a word in a mail to an actual count of these words, e.g., if the word at index \(i=0\) appears twice, then \(v[i] = 2\), could yield better results. We have no way to know beforehand, unless we also learn this embedding from the data at hand. If you want to know more, you might find the resources listed in the Projet Informatique 7 (see Moodle).
Conversely, once we have a powerful classifier between spam and ham, the natural question that arises is how to characterize both classes using very simple rules, e.g., “if we have \(X\) times a word from [this list], then 95 % of the time it’s spam”. However, deducing such rules from a 1899-dimensional space is not easy … This is one possible reason to use dimension reduction techniques (among others). See the bonus section and the separate theory webpage for an introduction to the simplest dimension reduction technique: random projections.